As an epidemic takes hold, reliable projections of its path and of its eventual size are important to health care providers and policy makers, in order to help them meet the challenge of organizing medical resources to meet treatment requirements. The many unknowns surrounding the COVID-19 virus make it particularly important and urgent to have reliable estimates of the future course of the daily numbers of new cases and deaths.
Epidemiological models that seek to estimate epidemic trajectories fall into two broad classes. One class, called compartmental models, consists of models that seek to be faithful to the details of the routes and processes of disease transmission. More specifically, they project how individuals in an initially susceptible population come to be exposed to the virus, potentially infected, and, if infected, either recover from the disease or die of it. This class of models is used to understand the consequences of policies, for example, a lockdown. But many aspects of the transmission and progress of the disease are unknown, and so these models, which are inevitably complex, are typically forced to rely on a large number of assumptions.
Time series models on the other hand, simply use historical data to make predictions. This paper develops a new class of time series models that reflect epidemic trajectories even when they change over time. This is done be allowing the logarithm of the growth rate of the cumulative series, which follows a downward time trend, to be time-varying. Seasonal or day of the week effects can be readily incorporated in the model. The latter are seen to be relevant in application. Unlike most standard time series models, the new models are able to make good forecasts even before new cases and/or deaths reach their peak. Furthermore they are able to track the epidemic as human behaviour changes, and can be used to evaluate the effects of changes in policy. Applying these models to the study of COVID-19 dynamics in the United Kingdom and Germany, we illustrate their relative simplicity and transparency, as well as their ability to produce good forecasts.
Although the focus of the paper is on the spread of epidemics, and specifically COVID-19, the models are applicable in a wide range of disciplines.
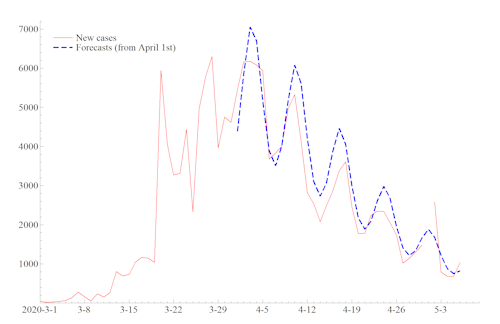
Forecasts (dashed - blue) for new cases in Germany using data (solid - red) up to March 31st. There was no observation reported for May 1st. The observation for May 2nd can be regarded as the sum of observations for May 1st and 2nd.
Read the paper in full:
Harvey, A. C. and P. Kattuman (2020). Time Series Models Based on Growth Curves with Applications to Forecasting Coronavirus, Harvard Data Science Review, Special Issue 1 – Covid-19.
Related papers:
Harvey, A. and Kattuman, P. (2021). A farewell to R: time-series models for tracking and forecasting epidemics, Journal of the Royal Society Interface, 18: 20210179. Earlier version in Covid Economics, 2020.
Harvey, A. C., Kattuman, P. and Thamotheram, C. (2021). Tracking The Mutant: Forecasting and Nowcasting COVID-19 in the UK in 2021, National Institute Economic Review, 256: 1, 110-126.
Harvey, A. C. (2021). Time Series Models for Epidemics: Leading Indicators, Control Groups and Policy Assessment, National Institute Economic Review (forthcoming).
Harvey, A. C. (2021). Time Series Modeling of Epidemics: Leading Indicators, Control Groups and Policy Assessment, Cambridge Working Papers in Economics 2114.
Professor Harvey and Dr Kattuman's research was featured in the following media outlets:
NIESR will be producing weekly updates on Thursdays, projecting new cases and estimating the R number using a class of time series models developed by Prof. Andrew Harvey and Dr. Kattuman
The HDSR paper on Covid modelling was listed as Highly Commended in the category “Academic research with real-world impact” in The Financial Times annual Responsible Business Education Awards announced in January 2023:
https://www.ft.com/content/679f19bd-92eb-475c-9eb2-7dbc9b82846e

About the authors
Professor Andrew Harvey is Emeritus Professor of Econometrics at the Faculty of Economics, University of Cambridge and Fellow of the Econometric Society and a Fellow of the British Academy (FBA). His research expertise is in Time Series, Financial Econometrics, State Space Models, Signal Extraction, Volatility.
Dr. Paul Kattuman is Reader in Economics at Cambridge Judge Business School, and Fellow, Corpus Christi College, University of Cambridge. His research interests are in Applied Econometrics and Statistics. Since the beginning of the pandemic he has been working closely with Public Health England along with a team from Judge Business School, providing policy relevant analysis for managing health care resources.