We estimate a SEIRD (susceptible-exposed-infected-recovered-deaths) epidemic model of COVID-19, which accounts for both observed and unobserved states and endogenous mobility changes induced by lockdown policies.
The model is estimated on Lombardy and London – two regions that had among the worst outbreaks in the world – and used to predict the evolution of the disease under different policies. We show that policies targeted also at mitigating the probability of contagion are more effective in containing the spread of the disease, than the one aimed at just gradually reducing mobility restrictions. In particular, we show that if the probability of contagion is decreased between 20% and 40% of its original level before the outbreak, while increasing mobility, the total death toll would not be higher than in a permanent lockdown scenario. On the other hand, their neglection could increase the risk of a second epidemic peak even while lifting lockdown measures at later dates. This highlights the importance, during the containment phase of the disease, of promoting also “soft” policy measures that could reduce the probability of contagion, such as, wearing masks and social distancing.
The novel coronavirus disease (COVID-19) spread quickly around the world. Many governments have adopted draconian measures to weaken its transmission among the population and some were more successful than others in containing its spread. The adoption of lockdown measures was deemed as necessary when policymakers realized that the virus was more infectious than initially thought, which brought many healthcare systems at the peak of the epidemic contagion to be under serious pressure. At some point the pressure on hospitals, and in particular on intensive care units, was so high that in some cases not all patients were treated. As a consequence, some people died without being diagnosed the infection and they did not enter the official death count. This implies that, in many countries, the official death toll considerably underestimates the true number of deaths. This happens in addition to under-reporting of cases in official statistics. Two clear examples of the under-reporting of both cases and deaths are Lombardy and London. Lombardy is the region in Northern Italy where the first cases of COVID-19 appeared in late February and it is by far the most severely hit region in Italy: as of May 2, with more than 14,000 deaths, it represents 49.4% of the Italian total death toll. In some provinces, though, the true death count is at least twice the official figure, reflecting the difficulties of the healthcare system to cope with the exponential spread of the disease and of intensive care units in admitting all patients that needed medical care, as highlighted also in the media. At the same time, many deaths happened in residential care homes, where many patients were not tested and, therefore, their death was not counted as COVID-19 related. Similarly, London accounts for the majority of deaths in the United Kingdom (approximately 25% of the official death toll), resulting in one of the epicentres of the disease in Europe. And in the UK the official death toll may be severely underestimated, as well.
The under-reporting of both cases and deaths suggests that, when trying to model the evolution of the disease, it is of utmost importance to take into account both observed and unobserved infections and deaths. To this end, we develop a compartmental susceptible-exposed-infected-recovered-deaths (SEIRD) model with two main types – observed and unobserved – of infections, recoveries and deaths. The model is used to forecast the evolution of the epidemic under a number of different scenarios. We calibrate the model on official data for Lombardy and London.
Besides accounting for the underestimation of total cases and deaths, our model incorporates endogenous mobility changes due to lockdown policies. Specifically, we decompose the infection rate of the disease – i.e. the rate at which susceptible individuals get exposed to the disease – in the product of two components:
- the average daily contact rate, which depends on mobility;
- the probability of contagion, i.e. the rate at which individuals infect each other, which crucially depends on how they comply with “soft” policies, such as wearing masks in public and social distancing.
We use mobility trends in Lombardy from Pepe et al. (2020) and in London from Google Community Mobility Reports to explicitly model lockdown by accounting for the decrease in mobility of individuals after its imposition.
Our model suggests that at the end of the fit period used to estimate the parameters (9 April in Lombardy, 15 April in London), the prevalence of the disease is approximately 5.7% in Lombardy and 2% in London. The number of unobserved infected cases is at least twice as large as observed cases in both regions, whereas the number of unobserved recoveries is between 20 and 26 times larger than observed recoveries. The true death count is underestimated by 35% in Lombardy and 17% in London.
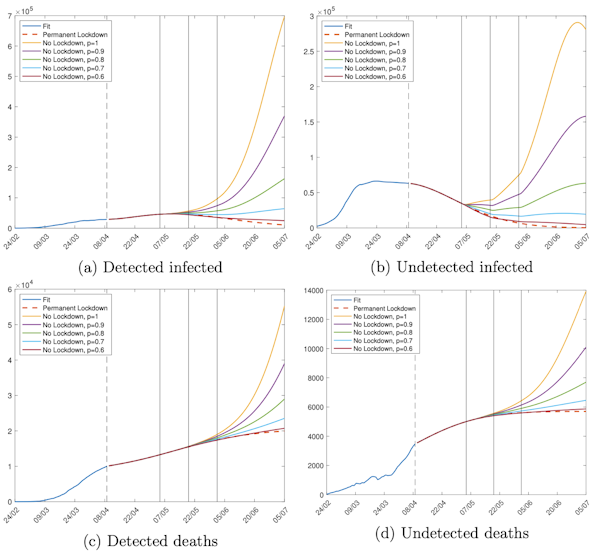
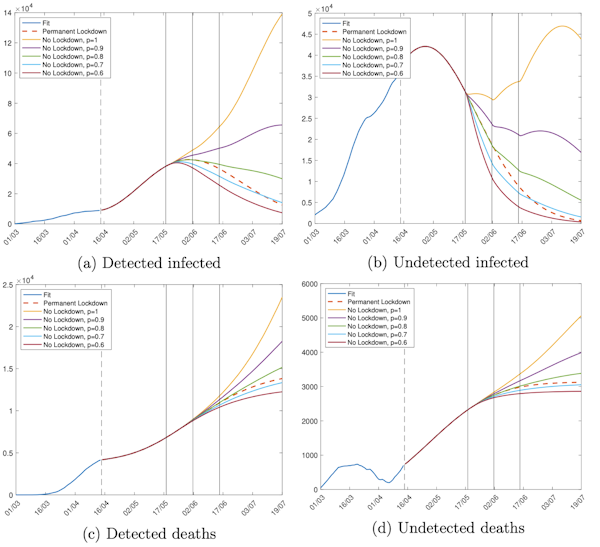
We use our model to forecast the evolution of the disease under different policy scenarios. Specifically, we assume that mobility restrictions are gradually lifted on three dates: May 4, May 18 and June 1 in Lombardy (as from government’s plans) and May 18, June 1, June 15 in London (two weeks later than Italy). On these dates, we assume mobility goes back to 25%, 50% and 75% of its pre-lockdown level. If the probability of contagion remains unaffected, we can expect a second peak of the epidemic and a resurgence in the death toll relative to a permanent lockdown scenario, as shown in Figures 1 and 2, that report for Lombardy and London, respectively, the evolutions of detected and undetected infected (panels a and b) and detected and undetected deaths (panels c and d). However, if the probability of contagion decreases, a second epidemic peak becomes less likely. In particular, if the probability of contagion is reduced by 40% relative to the baseline in Lombardy and between 20% and 30% in London, the expected death toll is in line with that of a permanent lockdown scenario.
Figure 1. Number of observed and unobserved deaths and infections in Lombardy under different assumptions on the probability of contagion
Figure 2. Number of observed and unobserved deaths and infections in London under different assumptions on the probability of contagion
In other terms, with appropriate policies that reduce the probability an individual is infected – e.g. social distancing, using masks, increasing hygiene standards, isolating infected cases –, we show that gradually and carefully lifting lockdown measures does not imply a resurgence of the epidemic curve. Our model suggests that the trade-off between economic recovery and saving lives can be balanced by implementing “soft” containment measures that could reduce the spread of the virus, even in the presence of increased mobility. On the other hand, their neglection could increase the risk of a second epidemic peak even while lifting lockdown measures at later dates. Our results may provide guidance to policymakers when deciding how and when lifting lockdowns.
Read the paper in full: Lifting Restrictions with Changing Mobility and the Importance of Soft Containment Measures: A SEIRD Model of COVID-19 Dynamics
References
Kermack, W. O. and McKendrick, A. G. (1927). A contribution to the mathematical theory of epidemics. Proceedings of the royal society of london. Series A, Containing papers of a mathematical and physical character, 115(772):700–721.
Pepe, E., Bajardi, P., Gauvin, L., Privitera, F., Lake, B., Cattuto, C., and Tizzoni, M. (2020). COVID-19 outbreak response: a first assessment of mobility changes in Italy following national lockdown. medRxiv.

About the authors
Salvatore Lattanzio is a PhD student at the Faculty of Economics, University of Cambridge. His research interests are in the area of Labour Economics, Inequality, and the Gender Wage Gap.
Dario Palumbo is a Bye-Fellow in Economics at Homerton College, University of Cambridge and Carlo Giannini Research Fellow in Econometrics at Ca' Foscari University of Venice. His research interests are in the area of Time Series, Circular Data, Heavy Tailed Distribution and Financial Econometrics.